5.4 Rational Functions
Introduction
Some observable characteristics, such as eye and hair color, are controlled by genes that pass from parent to child. It's not unusual for a trait to skip generations and appear to pop up out of nowhere. For instance, two people who don't have red hair can have redheaded children, or someone might have blue eyes even if both parents have brown eyes.
Since rational functions are built with polynomials, they inherit some of the same behaviors as their "parents", the polynomials. But rational functions also have several properties that polynomials do not have.
Rational Functions
In Chapter 4 we saw that dividing two polynomials $n$ and $d$ resulted in a new type of function called a rational function.
[ r(x)=\frac{n(x)}{d(x)} ]
The graphs of rational functions have some of the most complicated behavior we have seen so far.
As you can see from these examples, rational functions often have x-intercepts, a property they share with polynomials, but they can also have vertical and horizonal asymptotes, two things polynomials never have. There is even a entirely new behavior that we have not seen before that seems to pop up almost out of nowhere.
Zeros
Rational functions inherit their zero behavior from the polynomial in the numerator. You can explore this in the figure below. Look carefully at the link between the location of the zero and the factors in the numerator.
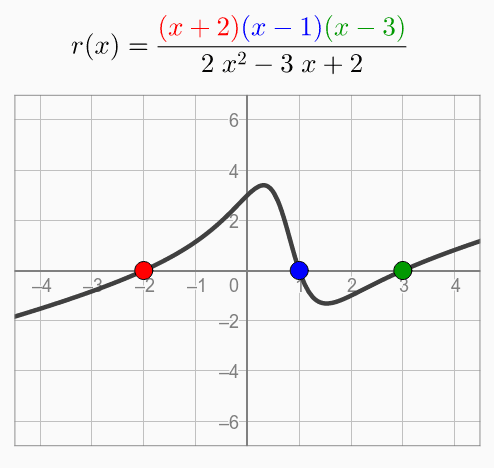
To use the interactive figure visit https://www.geogebra.org/m/hrgyn3qw
QUICK CHECK
- How can you find the x-intercepts of a rational function by looking at its equation?
Answer
If $(x-c)$ is a factor of the numerator, then the function has an x-intercept at $x=c$. The zeros of the polynomial in the numerator cause the zeros of the rational function.
Vertical Asymptotes
The vertical asymptotes of a rational function are caused by the polynomial in the denominator. In the figure below you can move the vertical asymptotes (indicated by the dotted lines). Look for a connection between the location of the vertical asymptotes and the factors in the denominator.

To use the interactive figure visit https://www.geogebra.org/m/ssgbhywx
QUICK CHECK
- How can you tell if a rational function has a vertical asymptote, just by looking at its equation?
Answer
If $(x-c)$ is a factor of the denominator, then the function has a vertical asymptote at $x=c$. The zeros of the polynomial in the denominator cause the vertical asymptotes of the rational function.
Removable Discontinuities
So far we've determined that zeros in the numerator cause x-intercepts while zeros in the denominator cause vertical asymptotes. But what would happen if there was a zero in both at the same place?
Or to ask the question another way, what is $\frac{0}{0}$? One thought is that it should equal $1$, since a number divided by itself is $1$. Another argument is that it should be $0$, since $0$ divided by any number is $0$.
But if we look back at what division means it gets even more complicated. Remember that $a \div b = x$ means $a = b \times x$.
Then $0 \div 0 = x$ would mean $0 = 0 \times x$, but that's true for every number! Since there's no single well defined way to say what $0 \div 0$ equals, we leave it undefined.
So whenever we have a rational function that has matching factors in the numerator and denominator, the graph is undefined at that point and there is a hole or break in the graph. The official term is "removable discontinuity".
In the figure below you can change the locations of the zero, the vertical asymptote, and the hole.

To use the interactive figure visit https://www.geogebra.org/m/ntYzprQz
QUICK CHECK
-
Identify all of the x-intercepts, vertical asymptotes and holes of the rational function [r(x)=\frac{(x-5)(x+3)(x-1)}{(x-2)(x-7)(x-1)}]
Answer
There are x-intercepts at $x=5, x=-3$, vertical asymptotes at $x=2, x=7$ and a hole at $x=1$. -
Write an equation for a rational function that has a zero at $x=2$, a vertical asymptote at $x=11$, and a hole at $x=4$.
Answer
[r(x)=\frac{(x-2)(x-4)}{(x-11)(x-4)}]
Horizontal Asymptotes
In addition to x-intercepts, vertical asymptotes and holes, rational functions often have horizontal asymptotes.
Recall that a horizontal asymptote is a long-term behavior, describing how the function levels off as $x \rightarrow \pm \infty$. Since the long-term behavior of a polynomial is controlled by the degree and leading coefficient, we should focus our attention on the degree and leading coefficients of the polynomials that make up a rational function.
In this first figure both polynomials have the same degree. Adjust the leading coefficients and see how that impacts the location of the horizontal asymptote.

To use the interactive figure visit https://www.geogebra.org/m/u76wmebr
As you've just seen, if the degrees match then you can simplify the leading coefficients to find the horizontal asymptote.
But what if the degrees do not match? In this figure you can alter the degree of each polynomial.

To use the interactive figure visit https://www.geogebra.org/m/prrwdbcz
If the degree of the numerator is larger, then no horizontal asymptote exists. However, if the degree of the denominator is larger, the horizontal asymptote is automatically at $y = 0$ (i.e. the x-axis).
QUICK CHECK
-
What is the horizontal asymptote of this rational function? [ r(x)=\frac{10x^3+4}{2x^3-8x^2} ]
Answer
Since the degrees match, the horizontal asymptote is $y=\frac{10}{2}=5$. -
What is the horizontal asymptote of this rational function? [ r(x)=\frac{5x-2}{3x^2+97x+13} ]
Answer
Since the degree on the bottom is larger, the horizontal asymptote is $y=0$. -
What is the horizontal asymptote of this rational function? [ r(x)=\frac{x^{6974}+1}{x^{3827}-4x} ]
Answer
Since the degree in the numerator is larger, there is no horizontal asymptote.

