5.3 Applications of Polynomials
Introduction
Located in the foothills of the Sierra Nevada mountains in the Andalusia region of Spain, the Alhambra palace is a world heritage site from the 13th century. Among it's most photographed features today are the water fountains in the Generalife gardens.
The water that flows out of these fountains follows a curved path through the air. But it's not just any random curve, it is a parabola!
Projectile Motion
It was Galileo who proved that any object launched into the air will follow the path of a parabola.
Drawings from Galileo's notebook showing results of his free fall experiments, dating from about 1609.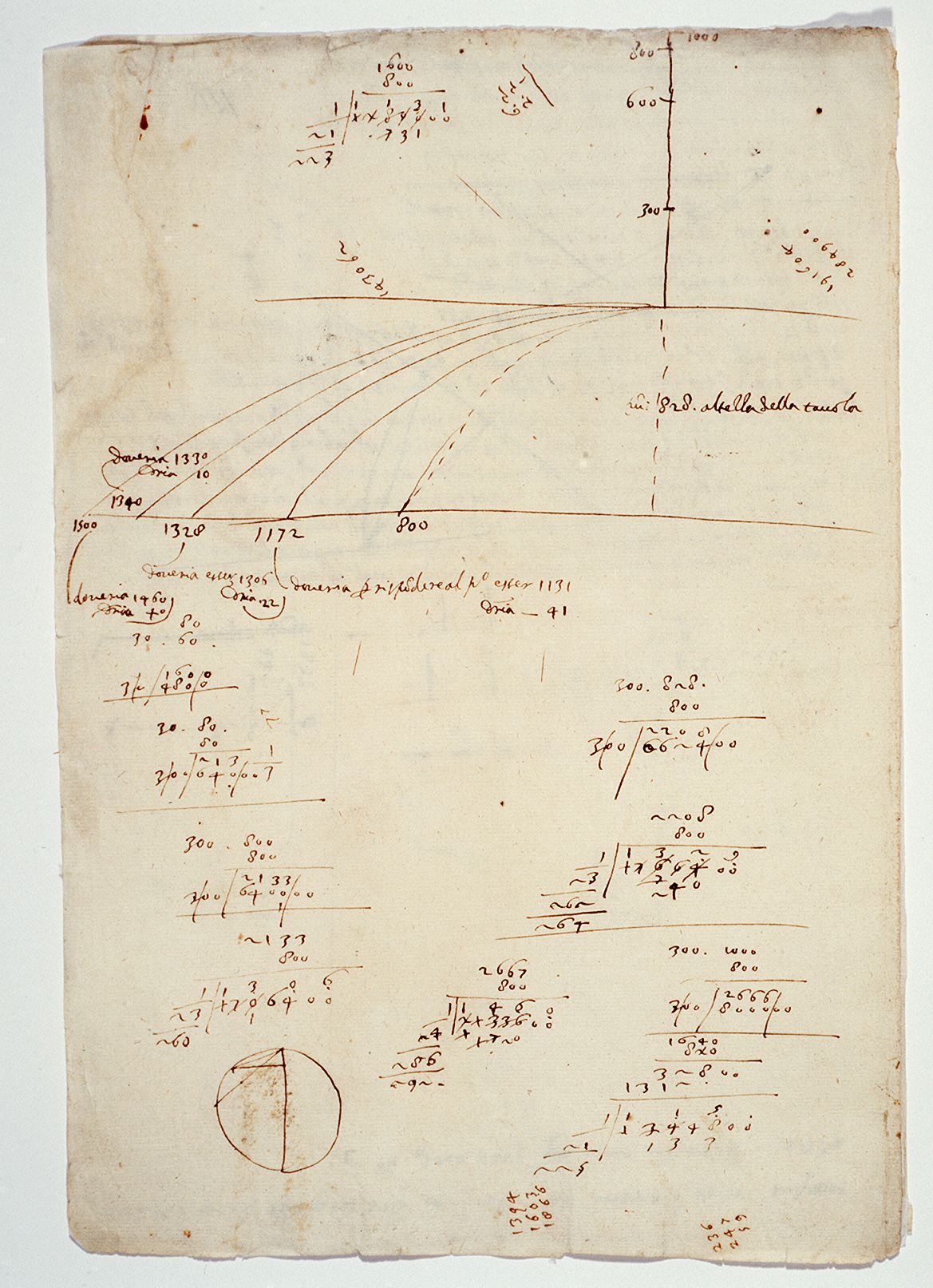 
This could be water tossed into the air by a fountain or a ball throw by a child, they all take on the same characteristic arc.
Physicists have studied this for hundreds of years and have discovered several equations that model the motion of projectiles. In particular, the vertical height of a projectile (in meters) can be written as a function of time
[ h(t) = -4.9 t^{2} + v t + h ]
where $v$ is vertical velocity (in meters per second), $h$ is the initial height (in meters) and $t$ is the time (in seconds).
QUICK CHECK
Suppose the skier in this photo leaves the jump with a vertical velocity of $2$ meters per second from a initial height of $70$ meters. Write an function that models their height, assuming the jump follows projectile motion.
Answer
Using $v=2$ and $h=70$ the function would be [ h(t)=-4.9t^{2}+2t+70 ]Finding the Vertex of a Parabola
One place where projectile motion is used is in the sport of pumpkin chuckin', where teams build slingshots, catapults or air cannons (like the one below) to throw pumpkins as far as possible.
If pumpkins leave the barrel of this air cannon 6.4 meters above the ground with a vertical velocity of 170 meters per second, then the height at any time is given by
[ h(t) = -4.9 t^{2} + 170 t + 6.4 ]
Our model gives the height at any time, so only questions involving height and time are fair game.
The obvious question of how far the cannon can shoot a pumpkin is, unfortunately, not one we can solve with this function.
Distance depends on the launch angle and you have to use trigonometry to find it. But to give you some idea, the current world record is well over one mile!
The two that come to mind are determining when the pumpkin will come back down and hit the ground and finding its maximum height.
Graphing our function will give us a better idea of where to look for the answers.
The pumpkin will come back down and hit the ground when the height is $0$, which means we need to find the zeros of the function. All that needs to be done is to solve $0= -4.9 t^{2} + 170 t + 6.4$ using the quadratic formula like we've done before.
[ \begin{align} t &= \frac{-b\pm\sqrt{b^2-4ac}}{2a} \newline &= \frac{-(170)\pm\sqrt{(170)^2-4(-4.9)(6.4)}}{(2)(-4.9)} \newline &= \frac{-170\pm\sqrt{29025.44}}{-9.8} \newline &= -0.0376 \small \text{ and } \normalsize 34.731 \small \text{ seconds} \newline \end{align} ]
Of the two values the only one that makes physical sense is $t=34.731$ seconds, which also matches the value in our graph.
The maximum height occurs at the peak of the graph which, for a parabola, is called the vertex. Due to symmetry, the vertex always occurs halfway between the two x-intercepts. In other words, if $x_1$ and $x_2$ are the two x-intercepts, then the x-coordinate of the vertex is $x_v=\frac{x_1+x_2}{2}$.
For our particular pumpkin cannon function $h(t) = -4.9 t^{2} + 170 t + 6.4 $ which had x-intercepts of $-0.0376$ and $34.731$, the x-coordinate of the vertex is
[ \begin{align} x_v & =\frac{x_1+x_2}{2} \newline &= \frac{-0.0376 + 34.731}{2} \newline &= 17.347 \end{align} ]
So our maximum height occurs $17.347$ seconds after launch.
To figure out what that height is, we put this time into the function
[ \begin{align} h(t) &= -4.9 t^{2} + 170 t + 6.4 \newline h(17.347) &= -4.9(17.347)^{2} + 170(17.347) + 6.4 \newline &= 1480.9 \small \text{ meters} \end{align} ]
and find that the maximum height is $1480.9$ meters.
Using the x-intercepts to find the vertex always works, but there is a faster method.
If your function is quadratic polynomial written as $f(x)=ax^2+bx+c$, then the x-coordinate of the vertex is always $x_v=\frac{-b}{2a}$ and the y-coordinate is $y_v=f(x_v)$.
Let's go back to the pumpkin function $h(t) = -4.9 t^{2} + 170 t + 6.4$ and see how this works.
The x-coordinate of the vertex is found by computing
[ \begin{align} x_v &=\frac{-b}{2a} \newline &= \frac{-170}{(2)(-4.9)} \newline &= 17.347 \end{align} ]
which is the same value as before, but we did not need to go through the quadratic formula to find the two zeros and locate the halfway point between them.
Getting the y-coordinate of the vertex is exactly the same as before, we just evaluate the function when $x=17.347$.
[ \begin{align} y_v &= f(x_v) \newline &= f(17.347) \newline &= -4.9(17.347)^{2} + 170(17.347) + 6.4 \newline &= 1480.9 \small \text{ meters} \end{align} ]
This technique for finding the vertex works on any quadratic function, not just with projectile motion. One thing to keep in mind, however, is that the vertex is not always a maximum. Depending on the shape of the parabola it could be a minimum.
QUICK CHECK
Suppose the motorcyclist in this photo leaves the ramp with a vertical velocity of 14 meters per second from a initial height of 2 meters. Write an function that models their height, assuming the jump follows projectile motion. Then find their maximum height by locating the vertex of your function.
Answer
Using $v=14$ and $h=2$ the function would be [ h(t)=-4.9t^{2}+14t+2 ] The x-coordinate of the vertex is [ \begin{align} x_v &=\frac{-b}{2a} \newline &= \frac{-(14)}{(2)(-4.9)} \newline &= 1.43 \small \text{ seconds} \end{align} ] and the y-coordinate of the vertex is [ \begin{align} y_v &= f(x_v) \newline &= f(1.43) \newline &= -4.9(1.43)^2+14(1.43)+2 \newline &= 12 \small \text{ meters} \end{align} ] So the motorcycle reaches a maximum height of 12 meters 1.429 seconds after leaving the ramp.Solving Quadratic Equations
Cliff diving is potentially a very dangerous sport. One maneuver that makes it a bit safer is called a barani.
The barani is a gymnastics move that combines a half somersault with a half twist. Performing a barani gives the diver time to see the water and control their landing so that they hit the water feet first.
Assuming a professional cliff diver can jump up with a vertical velocity of $3$ meters per second, then the projectile motion function
[ h(t)=-4.9 t^{2} + 3t + 27 ]
gives us their height above the water $t$ seconds after diving off the $27$ meter platform.
If a diver can complete a barani about 5 meters above the surface of the water, then the chance of a safe dive is very high. How much time does that give them to do their flips and twists?
To answer this we have to find $t$ so that $h(t)=5$. Setting up the equation we find that
[ \begin{align} h(t) &= 5 && \small \color{#5fa2ce}{\text{Original equation}} \newline -4.9 t^{2} + 3t + 27 &= 5 && \small \color{#5fa2ce}{\text{Insert equation for $h(t)$}} \newline -4.9 t^{2} + 3t + 22 &= 0 && \small \color{#5fa2ce}{\text{Subtract $5$}} \end{align} ]
which is another situation for the quadratic formula.
[ \begin{align} t &= \frac{-(3)\pm\sqrt{(3)^2-4(-4.9)(22)}}{2(-4.9)} && \small \color{#5fa2ce}{\text{Apply Quadratic Formula}} \newline t &= \frac{-3\pm\sqrt{440.2}}{-9.8} && \small \color{#5fa2ce}{\text{Simplify}} \newline t &= -1.84 \small \text{ and } \normalsize 2.45 \small \text{ seconds } && \small \color{#5fa2ce}{\text{Evaluate}} \end{align} ]
Clearly $t=-1.84$ seconds can't be our answer, so it must be that the diver has $2.45$ seconds to do their dive and complete the barani.
