4.2 Multiplication and Division of Functions

Introduction

The strong winds of large tropical storms, like hurricane Katrina or super storm Sandy, can push sea water toward the shore causing severe flooding. These "storm surges" are often a greater threat to life and property than the hurricane itself. The surge after Katrina reached 28 feet above flood level.

In this section we will see a simplified model for storm surges that results from multiplying a power function by an exponential decay function.

Combining Functions by Multiplication

In the last section we saw that if $f$ and $g$ are both functions, then we can form new functions by taking their sum $f+g$ or their difference $f-g$. The product of two functions $fg$ is also a function and can be evaluated using the rule

[ (fg)(x)=f(x)g(x) ]

In the table below, use the given values of $\color{red}{f(}x\color{red}{)}$ and $\color{blue}{g(}x\color{blue}{)}$ to find values for $(fg)(x)$.

$x$	$\color{red}{f(}x\color{red}{)}$	$\color{blue}{g(}x\color{blue}{)}$	$(fg)(x)=\color{red}{f(}x\color{red}{)}\color{blue}{g(}x\color{blue}{)}$
$1$	$\color{red}{4}$	$\color{blue}{9}$	$\color{red}{(4)}\color{blue}{(9)}=36$
$2$	$\color{red}{3}$	$\color{blue}{-5}$	Answer $\color{red}{(3)}\color{blue}{(-5)}=-15$
$3$	$\color{red}{1}$	$\color{blue}{14}$	Answer $\color{red}{(1)}\color{blue}{(14)}=14$
$4$	$\color{red}{-8}$	$\color{blue}{-3}$	Answer $\color{red}{(-8)}\color{blue}{(-3)}=24$
$5$	$\color{red}{-32}$	$\color{blue}{0}$	Answer $\color{red}{(-32)}\color{blue}{(0)}=0$

Notice that each $x$ creates only one $(fg)(x)$ value, which means that multiplying two functions always creates a new function.

The Domain of $(fg)(x)$

As with the sum and difference, the domain of $fg$ is the intersection of the domains of $f$ and $g$.

For example, if $f(x)=\ln(x)$ and $g(x)=4-x^{2}$, then

[ \begin{align} (fg)(x) &= \ln(x)(4-x^{2}) \newline &= 4\ln(x)-x^{2}\ln(x) \end{align} ]

Since $f(x)=\ln(x)$ is only defined for positive values of $x$, the product $f g$ is only defined for $x>0$ as well.

Simplifying $(fg)(x)$

Sometimes we can tell what type of function the product $f g$ will be by recognizing what type of function $f$ and $g$ are.

When $f$ and $g$ are Power Functions

Suppose you take two power functions, like $\color{red}{f(x)=x^{1.3}}$ and $\color{blue}{g(x)=x^{2.5}}$. Their product is also a power function

[ \begin{align} (f g)(x) &= \color{red}{x^{1.3}}\color{blue}{x^{2.5}} \newline &= x^{3.8} \end{align} ]

When $f$ and $g$ are Exponential Functions

A similar thing holds if $f$ and $g$ are both exponential functions. As an example, consider $\color{red}{f(x)=2^{x}}$ and $\color{blue}{g(x)=3^{x}}$. The equation for $f g$ is

[ \begin{align} (f g)(x) &= \color{red}{2^{x}}\color{blue}{3^{x}} \newline &= 6^{x} \end{align} ]

which is also an exponential function.

When $f$ and $g$ are Polynomials

Lastly, the product of two polynomials is still a polynomial. Using $\color{red}{f(x)=3x+1}$ and $\color{blue}{g(x)=x+4}$, for instance, gives

[ \begin{align} (f g)(x) &= \color{red}{(3x+1)}\color{blue}{(x+4)} \newline &= 3x^{2}+13x+4 \end{align} ]

Graphs of $(fg)(x)$

We can also gain some insight into the graph of $(fg)(x)$ by inspecting the graphs of $f(x)$ and $g(x)$.

Of particular interest is the fact that $(fg)(x)$ inherits the x-intercepts from both $f(x)$ and $g(x)$.

This can be explored in the interactive figure below. The $\color{red}{f(x)=4-x^{2}}$ and $\color{blue}{\ln(x)}$ are shown, though you can change either one.

It's worth noting that the product $fg$ only exists for $x>0$ since the domain of the logarithm is $x>0$.

Applications

At the start of this section we mentioned the storm surge following a tropical storm like a hurricane. It's now time that we looked at this shape and tried to find a function with a similar graph.

The chart below from the United States Geological Survey shows the storm surge for Hurricane Rita in 2005. Notice how the water level (in blue) increases quickly, and then recedes at a slower rate.

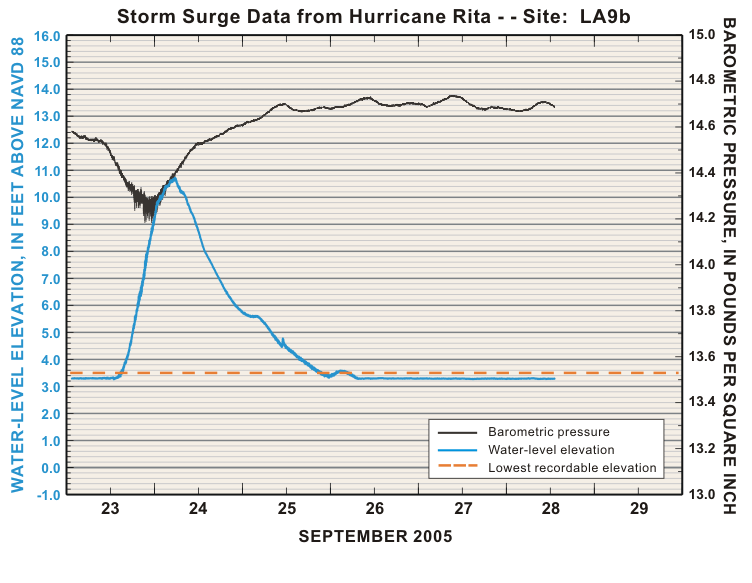
One way to create a function that grows quickly and then decays is to multiply an increasing power function by an exponential decay function.

In the figure below, the graphs of $f(x)=10x^{2}$ and $g(x)=e^{-x}$ are shown. The graph of $(fg)(x)=10x^{2}e^{-x}$ will be drawn as you change the value of $x$.

As you have just seen, the graph of the function $f(x)=10x^{2}e^{-x}$ is similar in some ways to storm surge flooding. In fact, functions of this type, where an increasing power function is multiplied by an exponential decay function, are often called surge functions. All surge functions have the form

[ f(x)=ax^{p}e^{-b x} ]

where $p>0$ and $b>0$. The rapid rise, or surge, is caused by the power function and the eventual decay is due to the exponential function.

Surge functions can be found in a number of areas. For instance, the level of glucose in your blood, the electrical current in a toy car, the number of Tweets about a world news event, or even the number of people trying to figure out how to watch the Superbowl online can display surge-like behavior.

Unfortunately, fitting a surge function to real data is beyond the scope of this book, but it's existence should illustrate the utility of creating new functions by multiplication. Division of functions is also useful, and that is where we turn our attention next.

Combining Functions by Division

Since we have worked with addition, subtraction and multiplication of functions, it should come as no surprise that dividing one function by another creates a new function. The quotient of two functions $f$ and $g$ is defined as

[ \left(\frac{f}{g}\right)(x)=\frac{f(x)}{g(x)} ]

provided that $g(x) \neq 0$.

Simplifying $\left(\frac{f}{g}\right)(x)$

If $f$ and $g$ are either both power functions or both exponential functions then the rules of exponents allow us to simplify their quotients.

You might recall that

[ \frac{x^m}{x^n}=x^{m-n} ]

where $m$ and $n$ are any real numbers and $x \neq 0$. In the present context, this shows that the quotient of any two power functions is just another power function, and that $x=0$ must be excluded from the domain of $x^{m-n}$.

Another rule of exponents states that

[ \frac{a^x}{b^x}=\left(\frac{a}{b}\right)^{x} ]

where $a$ and $b$ are any positive real numbers. This rule shows that the quotient of any two exponential functions is still an exponential function. And since $a$ and $b$ are positive, there are no restrictions on the domain of $\left(\frac{a}{b}\right)^{x}$.

Rational Functions

As we have just seen, division of power functions and division of exponential functions is simply an application of the rules of exponents.

In those cases division does not generate a new category of function--the quotient of two power functions is just another power function and the quotient of two exponentials is another exponential function.

However, dividing one polynomial by another polynomial does create a new family of functions, known as rational functions. A rational function is any function that can be written in the form

[ f(x)=\frac{n(x)}{d(x)} ]

where $n(x)$ and $d(x)$ are both polynomials and $d(x)\neq0$.

Graphs of Rational Functions

The graphs of rational functions can have very interesting and complex behaviors. The graphs below should give you an idea of the variety we might encounter.

In Chapter 5 we will examine the properties of rational functions. One tool that will help us do that is being able to simplify the equation by cancelling common terms, if possible, or by polynomial division.

Simplifying Rational Functions by Cancellation

Sometimes it is possible to simplify a rational function by canceling common factors. Whenever we cancel factors, we should keep in mind the domain of the original rational function.

For instance, the rational function $f(x)=\frac{x^{2}-3x}{x}$ can be simplified by canceling the $x$ that all terms have in common.

[ \begin{align} f(x) &= \frac{x^{2}-3x}{x} \newline &= \frac{x^{2}}{x} - \frac{3x}{x} \newline &= x-3 \end{align} ]

But we must remember to specify that this only holds for $x \neq 0$, since $0$ is not included in the domain of $f(x)=\frac{x^{2}-3x}{x}$. The proper way to write it is

[ f(x)=\frac{x^{2}-3x}{x}=x-3, \thinspace x \neq 0 ]

Without the condition that $x \neq 0$, this would be a false statement.

Simplify Rational Functions by Long Division

When no common factors can be found, a rational function can be simplified by division, but only if the polynomial in the numerator has a degree that is higher than or equal to the degree of the denominator.

For instance, $f(x)=\frac{x^{2}-3x}{x-1}$ and $f(x)=\frac{x^4-6x}{x^4+8}$ can be simplified by division while $g(x)=\frac{2x+4}{x^{3}-5}$ cannot.

You'll recall that dividing one whole number by a whole number divisor results in a quotient and a remainder. As an example,

[ \frac{15}{7} = 2 + \frac{1}{7} ]

were $7$ is the divisor, $2$ is the quotient and $1$ is the remainder.

Polynomial division follows the identical pattern:

[ \frac{n(x)}{d(x)}=q(x)+\frac{r(x)}{d(x)} ]

We refer to the function $d(x)$ as the divisor, $q(x)$ as the quotient and $r(x)$ as the remainder.

The traditional method for dividing one polynomial by another is called polynomial long division, and works much like long division of numbers. The figure below will walk you through the algorithm for dividing $3x^{2}+5x-2$ by $x+1$. Use the controls in the lower left corner to start or pause the process or skip directly to any step.

After performing the division we need to identify the divisor $d(x)$, the quotient $q(x)$ and the remainder $r(x)$.

Now we can simplify $\frac{3x^{2}+5x-2}{x+1}$ using the $\frac{n(x)}{d(x)}=q(x)+\frac{r(x)}{d(x)}$ pattern. The final result is

Now that you have seen an example, let's walk through another division problem together. This time we will divide $4x^{2}-5$ by $x+2$.

1. Write the problem as a long division.

   Answer

   ---

   

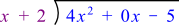
2. What multiplies $x$ to create $4x^{2}$?

   Answer

   ---

   $4x$

3. Perform the first step of the division.

   Answer

   ---

   

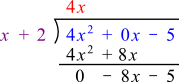
4. What is the next number that should go above the division symbol?

   Answer

   ---

   It needs to be a $-8$.

5. Perform the rest of the division.

   Answer

   ---

   

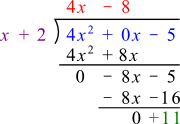
6. Now identify the quotient and remainder.

   Answer

   ---

   

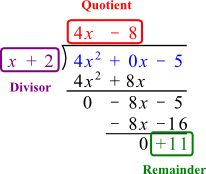
Synthetic Division

When the divisor is simple, something of the form $x-c$, such as $x-3$ or $x-5$, then the long division process can be greatly simplified. This simplified division process is called synthetic division. Synthetic division is simpler because we only work with the number $c$ from the divisor and the coefficients of the numerator.

For instance, if the divisor is $x-6$ then $c=6$, if the divisor is $x+8$ then $c=-8$.

If the numerator is $7x^{3}+5x-9$ then we work with the coefficients $7, 0, 5, -9$, including a $0$ for any term that is missing.

Whereas the long division algorithm required multiplication and then subtraction, with synthetic division we multiply and then add.

Earlier we used long division to divide $3x^{2}+5x-2$ by $x+1$. Here we perform the same calculation with synthetic division. Use the controls in the lower left corner to start or pause the process or skip directly to any step.

After identifying the divisor $d(x)$, quotient $q(x)$ and remainder $r(x)$.

we can rewrite $\frac{3x^{2}+5x-2}{x+1}$ as

using the $\frac{n(x)}{d(x)}=q(x)+\frac{r(x)}{d(x)}$ pattern.

Next we will divide $2x^{3}+7x^{2}-2x-12$ by $x+3$. Fill in the steps as prompted below.

1. What are the coefficients of the numerator?

   Answer

   ---

   

2. What is $c$?

   Answer

   ---

   

3. Write as a synthetic division.

   Answer

   ---

   

4. Complete the synthetic division.

   Answer

   ---

   

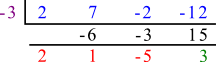
5. Identify the quotient and remainder.

   Answer

   ---

   

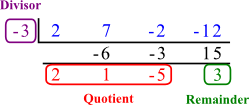
6. Use the quotient and remainder to simplify $\frac{2x^{3}+7x^{2}-2x-12}{x+3}$.

   Answer

   ---

   

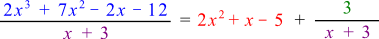
Looking Ahead

We now know how to combine functions using the four basic operations of addition, subtraction, multiplication and division. We've also seen how complicated behaviors, like those of polynomial and rational functions, can arise by combining simple functions.

We will return to polynomial and rational functions in the following chapter, but first we must investigate another way to combine functions.