3.5 Exponential and Logarithmic Equations
Introduction
Since exponential and logarithmic functions arise in many applications, it is essential to be able to manipulate and solve equations involving them. As an example of the type of problems we might encounter, consider the following situation.
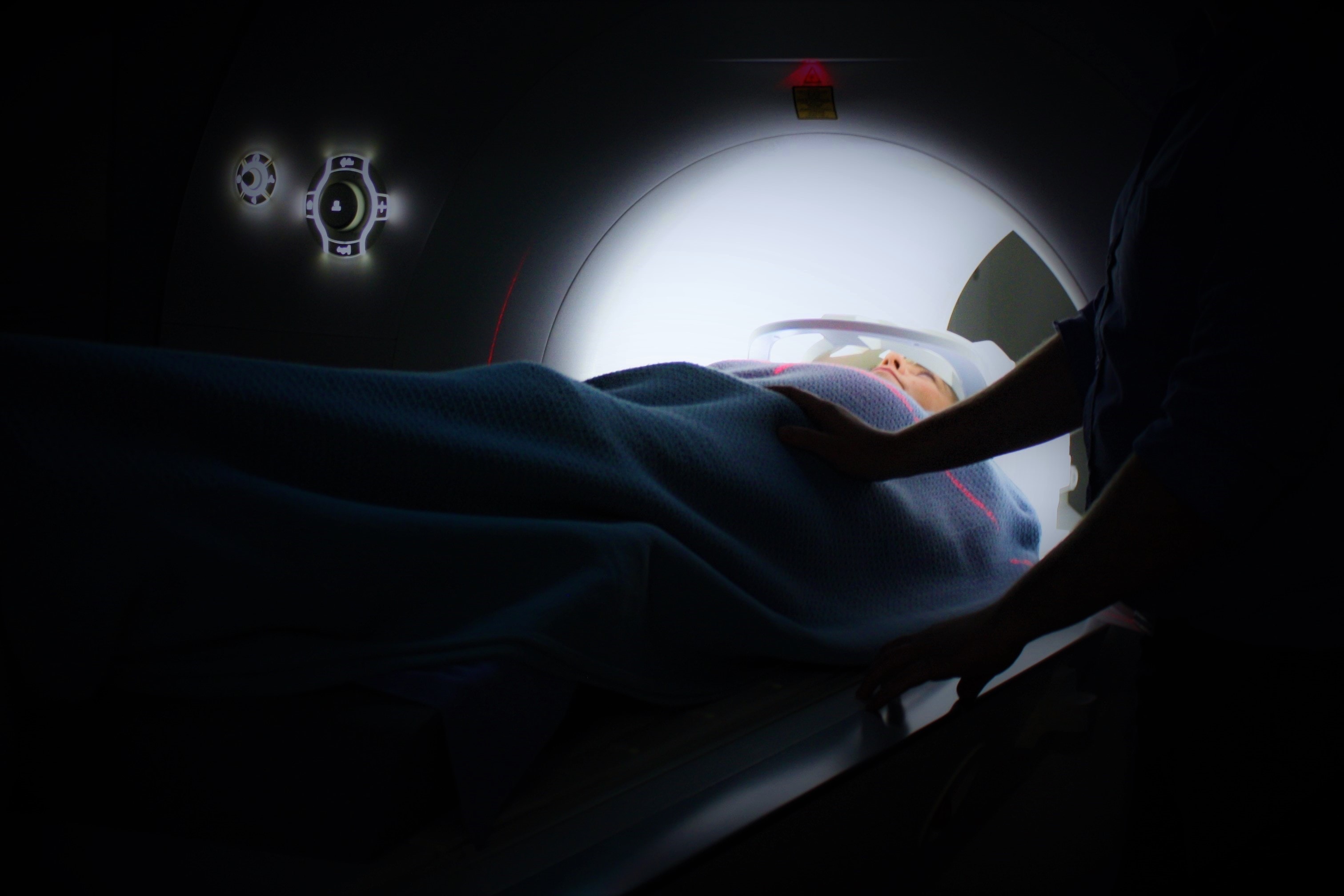
A patient who is undergoing diagnostic imaging for thyroid cancer typically swallows a capsule containing the radioactive isotope Iodine-123 shortly before being placed inside a scanner. The scanner detects radiation from the Iodine-123 and constructs a 3D image of the area being scanned, which is used by doctors to plan treatment options.
One of the main advantages of using Iodine-123 is that it has a relatively short half-life of approximately 13.2 hours. This means that within 13.2 hours, one-half of the Iodine-123 will be gone.
If a patient is given 400 microcuries of Iodine-123, how long will it take for the radiation level to drop to a negligible 10 microcuries?
To answer this question, we need to be able to solve the exponential half-life equation
[ 10=400\left(\frac{1}{2}\right)^{t/13.2} ]
In this section, we will learn techniques for solving equations like this, where the variable is in the exponent, as well as equations involving logarithms. Once we have established the basic techniques, we can return and solve questions like this one.
Techniques for Solving Exponential Equations
There are three main techniques for solving exponential equations. But before solving any exponential equation we should first isolate the exponential expression.
First Step: Isolate the Exponential
When working with more complicated exponential equations it is often necessary to perform some algebraic simplifications first in order to isolate the exponential expression.
As an example, let's examine the equation $500(1.2)^{x}=3000$. Here the exponential expression $(1.2)^{x}$ has been multiplied by $500$. If we divide both sides of the equation by $500$, then we will have isolated $1.2^{x}$.
[ \begin{align} 500(1.2)^{x} &= 3000 \newline 1.2^{x} &= 6 && \small \color{#5fa2ce} {\text{Divide by } 500} \newline \end{align} ]
At this point we can choose an appropriate solving technique from the choices discussed below. But this initial step of isolating the exponential is always an essential first step.
QUICK CHECK
-
What must be done to isolate the exponential in the equation $2^{x}+6=54$?
Answer
Subtracting $6$ from both sides will isolate the exponential. -
What must be done to isolate the exponential in the equation $4(3)^{x}=324$ ?
Answer
Dividing both sides by $4$ will isolate the exponential.
Solving Method 1: The One-to-One Property of Exponentials
One technique for solving an exponential equation is to take advantage of the fact that all exponential functions are one-to-one. This means that
[ b^N=b^M \text{ if and only if }N=M ]
So if we can express both sides of an equations as powers of the same base, then the one-to-one property tells us that the solution can be found by comparing the exponents.
For example, suppose we want to solve $7^{x+3}=49$. We can do so by writing both sides as powers of $7$ and equating the exponents.
[ \begin{align} 7^{x+3} &= 49 \newline 7^{x+3} &= 7^2 && \small \color{#5fa2ce}{{\text{Rewrite }} 49=7^2} \newline x+3 &= 2 && \small \color{#5fa2ce}{\text {One-to-one property of exponentials}} \newline x &= -1 && \small \color{#5fa2ce}{-3 \text{ from both sides}} \end{align} ]
Notice that this method only works when both sides can be written easily as powers of the same base. If the equation had been just slightly different, say $7^{x+3}=50$, we would not have been able to solve it easily with this technique.
QUICK CHECK
Solve the exponential equation $2^{x-1}=8$ by relating the bases.Answer
[ \begin{align} 2^{x-1} &= 8 \newline 2^{x-1} &= 2^{3} && \small \color{#5fa2ce}{\text{rewrite } 8=2^{3}} \newline x-1 &=3 && \small \color{#5fa2ce}{\text{since exponentials are one-to-one}} \newline x &= 4 && \small \color{#5fa2ce}{+1 \text{ to both sides}} \end{align} ]Solving Method 2: Rewrite as a Logarithmic Equation
Another useful technique is to rewrite an exponential equation as an equivalent logarithmic equation using the definition of a logarithm.
[ b^{x}=y \Longleftrightarrow \log_{b}(y) = x ]
For instance, if we start with the equation $3^{x}=10$ then rewriting it as a logarithm gives us the solution $x = \log_3{10}$, which could be evaluated using the change of base formula. [ \log_b(x)=\frac{\log(x)}{\log(b)}=\frac{\ln(x)}{\ln(b)} ] The complete process would look like this:
[ \begin{align} 3^{x} &= 10 \newline x &= \log_3(10) && \small \color{#5fa2ce}{\text{Rewrite as a log equation}} \newline x &= \frac{\ln(10)}{\ln(3)} && \small \color{#5fa2ce}{\text{Change of base formula}} \newline x & \approx 2.0959 && \small \color{#5fa2ce}{\text{Evaluate}} \newline \end{align} ]
We could have used $\log$ for the change of base formula and still arrived at the correct answer, but $\ln$ will be our default choice.
QUICK CHECK
How would you solve $5^{x}=200$ for $x$?Answer
[ \begin{align} 5^{x} &= 200 \newline x &= \log_5(200) && \small \color{#5fa2ce}{\text{Rewrite as a log equation}} \newline x &= \frac{\ln(200)}{\ln(5)} && \small \color{#5fa2ce}{\text{Change of base formula}} \newline x & \approx 3.292 && \small \color{#5fa2ce}{\text{Evaluate}} \newline \end{align} ]Solving Method #3: Take the Logarithm of Both Sides
Perhaps the most useful technique for solving an exponential equation is to take the logarithm of both sides.
For example, suppose we start with $3^{x}=10$ and take the natural log of both sides. [ \begin{align} 3^{x} &= 10 \newline \ln\left(3^{x}\right) &= \ln(10) && \small \color{#5fa2ce}{\text{Apply } \ln \text{to both sides}} \end{align} ]
While this might seem worse than the original equation, it is actually better because we can now apply the power rule for logarithms [ \log_b x^{p} = p \log_b (x) ] and bring the $x$ out of the exponent.
[ \begin{align} \ln\left(3^{x}\right) &= \ln(10) \newline x \cdot \ln(3) &= \ln(10) && \small \color{#5fa2ce}{\text{Power rule for logs}} \end{align} ]
The final step is to divide both sides by the number $\ln(3)$.
[ \begin{align} x \cdot \ln(3) &= \ln(10) \newline x &= \frac{\ln(10)}{\ln(3)} && \small \color{#5fa2ce} {\text{Divide by } \ln(3)} \newline x &\approx 2.0959 && \small \color{#5fa2ce} {\text{Evaluate}} \end{align} ]
Notice that the last two lines are exactly the same as when we solved this earlier with the change of base formula. One of the nice features of this technique is that the change of base formula is built in, so you do not need to memorize it.
QUICK CHECK
Solve the same equation $3^{x}=10$ using $\log$ instead of $\ln$. Verify that your decimal approximation is identical to the one found above.Answer
[ \begin{align} 3^{x} &= 10 \newline \log\left(3^{x}\right) &= \log(10) && \small \color{#5fa2ce}{\text{Apply } \log} \newline x \cdot \log(3) &= \log(10) && \small \color{#5fa2ce}{\text{Power rule for logs}} \newline x &= \frac{\log(10)}{\log(3)} && \small \color{#5fa2ce} {\text{Divide by } \log(3)} \newline x &\approx 2.0959 && \small \color{#5fa2ce} {\text{Evaluate}} \end{align} ]This method has an extra benefit if the base of the exponential in the equation is $e$.
If we start with the equation $e^{2x}=17$, as an example, then when taking the natural log of both sides we are able to use the inverse property of logs [ \log_b\left(b^x\right)=x ] rather than the power rule.
[ \begin{align} e^{2x} &= 17 \newline \ln\left(e^{2x}\right) &= \ln 17 && \small \color{#5fa2ce}{\text{Apply } \ln} \newline 2x &= \ln 17 && \small \color{#5fa2ce} {\text{Inverse property of logs}} \newline x &= \frac{\ln 17}{2} && \small \color{#5fa2ce} {\text{Divide by }2} \newline x &\approx 1.4166 && \small \color{#5fa2ce} {\text{Evaluate}} \end{align} ]
Notice how this simplifies the solving process, with the logarithm undoing the exponential.
Solve Applications Involving Exponential Equations
Half-Life
Now that we have established the basic techniques for solving exponential equations, let's return to the section opener.
We want to know how long it will take for the radiation level to drop to 10 microcuries given an initial dose of 400 microcuries of Iodine-123. Since we know that the half-life of Iodine-123 is 13.2 hours, we will use the half-life formula to write our equation:
[ 10=400\left(\frac{1}{2}\right)^{t/13.2} ]
Our task is to solve this equation for $t$. The first step is to isolate the exponential.
[ \begin{align} 10 &= 400\left(\frac{1}{2}\right)^{t/13.2} \newline \frac{10}{400} &= \left(\frac{1}{2}\right)^{t/13.2} && \small \color{#5fa2ce} {\text{Divide by } 400} \newline \end{align} ]
Now we have to decide which method to use to solve the equation. Since it is not obvious how to write both sides as powers of $\frac{1}{2}$, and converting it to a logarithm equation looks like it would be messy, let's take the natural logarithm of both sides.
[ \begin{align} \frac{10}{400} &= \left(\frac{1}{2}\right)^{t/13.2} \newline \ln \left(\frac{10}{400} \right) &= \ln \left(\frac{1}{2}\right)^{t/13.2} && \small \color{#5fa2ce} {\text{Apply } \ln} \newline \ln \left(\frac{10}{400} \right) &= \frac{t}{13.2} \ln \left(\frac{1}{2}\right) && \small \color{#5fa2ce} {\text{Power rule for logs}} \newline \frac{\ln \left(\frac{10}{400}\right)}{\ln \left(\frac{1}{2}\right)} &= \frac{t}{13.2} && \small \color{#5fa2ce} {\text{Divide by } \ln\left(\frac{1}{2}\right)} \newline t &= 13.2 \frac{\ln \left(\frac{10}{400}\right)}{\ln \left(\frac{1}{2}\right)} && \small \color{#5fa2ce} {\text{Multiply by } 13.2} \newline t &\approx 70.249 && \small \color{#5fa2ce} {\text{Evaluate}} \end{align} ]
This means that it will take 70.249 hours (roughly 3 days) for the radiation level to drop from 400 to 10 microcuries.
Doubling Time

When solving real life problems, we usually will not be given the equation directly. When this happens, we must construct it from the information available and our knowledge of appropriate models.
For instance, suppose you have invested $5000 in an account earning 2% interest compounded continuously. How long will it take for your investment to double?
Since this question involves continuously compounded interest, we should use the continuous growth model $A(t)=P e^{r t}$.
QUICK CHECK
Based on the information given, what are the values for $P$, $r$ and $A(t)$?Answer
The initial deposit is 5000 dollars, so $P=5000$. The rate is given as 2%, so $r=0.02$. The balance of the account should be double the initial deposit, so $A(t)=10000$. Substituting those values into $A(t)=P e^{r t}$ will let us solve for the time it takes for the investment to double.Making the substitutions $P=5000$ and $r=0.02$ we see that the account balance for any $t$ is given by $A(t)=5000e^{0.02 t}$. We need to find $t$ so that $A(t)=10000$.
[ \begin{align} 10000 &= 5000 e^{0.02 t} \newline 2 &= e^{0.02 t} && \small \color{#5fa2ce} {\text{Divide both sides by } 5000} \newline \ln(2) &= \ln(e^{0.02 t}) && \small \color{#5fa2ce} {\text{Apply } \ln \text{ to both sides}} \newline \ln(2) &= 0.02 t && \small \color{#5fa2ce} {\text{Use the inverse relationship } \ln(e^{x})=x} \newline \frac{\ln(2)}{0.02} &= t && \small \color{#5fa2ce} {\text{Divide both sides by } 0.02} \newline t &\approx 34.657 && \small \color{#5fa2ce} {\text{Decimal approximation}} \newline \end{align} ]
We have found that it will take close to 35 years for the investment to double if it earns 2% continuously.
QUICK CHECK
Rework the problem above assuming the initial deposit is just $70$ dollars. What is the doubling time? What does this tell you about doubling times in general? Once we divide by $70$, this is exactly the same as the problem above and has the same solution. Answer
| $140 =70 e^{0.02 t}$ | |
|---|---|
| $2 =e^{0.02 t}$ | Divide both sides by $70$ to isolate the exponential. |
| This shows that doubling time depends entirely on the rate, not on the size of the initial investment. |
Stock Price for Google
Let's consider a similar example. When Google went public in 2004 you could by a share of stock for $85 .
Just 2 years later, Google stock was trading at $387 per share. Assuming the price increased exponentially, what was the continuous rate of growth?
In this case, we will also use $A(t)=P e^{r t}$. We know $P=85$, $t=2$ and want to find $r$ so that $A(2)=387$.
| $387 = 85 e^{r(2)}$ | |
|---|---|
| $\frac{387}{85} =e^{2 r}$ | Divide both sides by $85$ to isolate the exponential. |
| $\ln\left(\frac{387}{85}\right) = \ln\left(e^{2 r}\right)$ | Apply the natural log $\ln$ to both sides. |
| $\ln\left(\frac{387}{85}\right) = 2 r$ | Use the inverse relationship $\ln(e^{x})=x$. |
| $\frac{\ln\left(\frac{387}{85}\right)}{2} = r$ | Divide both sides by $2$. |
| $r \approx 0.7579$ | Use a calculator to find a decimal approximation. |
This means that over the 2-year period from 2004 to 2006, Google's stock increased at a continuous rate of 75.79%.
Notice that while the numbers were different, the process of solving this equation was exactly the same as in the previous example. The only difference being that we were solving for $r$ instead of $t$.
Radioactive Decay

In 1912, men working in an English quarry discovered what appeared to be a prehistoric human skull. Piltdown Man, as the fossil was known, seemed to be a clear indication that the human species had originated in England and was considered by many to be the "missing link" in the history of human evolution. But was it really?
The age of fossils is often determined by a process called carbon dating. Plants absorb small amounts of the radioactive isotope carbon-14 from the atmosphere. People and animals collect carbon-14 when they eat plants and other animals. Once they die, however, the amount of carbon-14 begins to decay exponentially with a half-life of about 5730 years. By comparing the amount of carbon-14 in a fossil with the amount that would have been been present when it was alive we can estimate the fossil's age.
Suppose that you were able to get a small fragment of the bone and extract $9.7 \times 10^{-15}$ grams of carbon-14 out of it. If there would have been $1.05 \times 10^{-14}$ grams present when Piltdown Man was alive, how old is this fossil?
To solve this we will use the half-life formula $f(t) = a \left(\frac{1}{2}\right)^{t/c}$.
QUICK CHECK
Use the information above to write the equation that we must solve. Keep in mind that $a$ is the initial value, $c$ is the half-life, and $f(t)$ is the amount after some period of time.Answer
Taking $a = 1.05 \times 10^{-14}$, $c = 5730$ and $f(t) = 9.7 \times 10^{-15}$, the equation that must be solved is [9.7 \times 10^{-15} = 1.05 \times 10^{-14}\left(\frac{1}{2}\right)^{t/5730}]To determine the actual age of the Piltdown skull, we must use the half-life formula with $a=1.05 \times 10^{-14}$, $c = 5730$ and $f(t) = 9.7 \times 10^{-15}$. Our task is to solve for $t$.
| $9.7 \times 10^{-15} = 1.05 \times 10^{-14}\left(\frac{1}{2}\right)^{t/5730}$ | |
|---|---|
| $0.9238 = \left(\frac{1}{2}\right)^{t/5730}$ | Divide both sides by $1.05 \times 10^{-14}$ to isolate the exponential. |
| $\ln(0.9238) = \ln \left(\left(\frac{1}{2}\right)^{t/5730}\right)$ | Apply the natural log $\ln$ to both sides. |
| $\ln(0.9238) = \frac{t}{5730} \ln \left(\frac{1}{2}\right)$ | Use the power rule for logarithms. |
| $\frac{\ln(0.9238)}{\ln\left(\frac{1}{2}\right)} = \frac{t}{5730}$ | Divide both sides by $\ln\left(\frac{1}{2}\right)$. |
| $t = 5730 \frac{\ln(0.9238)}{\ln\left(\frac{1}{2}\right)}$ | Multiply both sides by $5730$. |
| $t \approx 655.21$ | Use a calculator to find a decimal approximation. |
As this result suggests, Piltdown Man was an elaborate forgery. Someone had cleverly stained and carved the bones to look old, though this fact was not discovered for more than 40 years. And while the perpetrator has never been determined, there are several suspects, including Sir Arthur Conan Doyle (author of Sherlock Holmes) who lived nearby. In any case, Piltdown Man remains one of the greatest unsolved scientific hoaxes of all time.
Nuclear Stockpile
During the 1950's, the number of active nuclear warheads in the U.S. arsenal doubled every 2.27 years. If there were 369 nuclear warheads in 1950, when did the U.S. stockpile exceed 30,000?
As we are given the doubling time, it makes sense to use the function $f(t)=a(2)^{t/c}$ with $a=369$, $c = 2.27$ and to try and find a $t$ so that $f(t)=30000$.
| $30000 =369(2)^{t/2.27}$ | |
|---|---|
| $\frac{30000}{369} = 2^{t/2.27}$ | Divide both sides by $369$ to isolate the exponential. |
| $\ln\left(\frac{30000}{369}\right) = \ln\left(2^{t/2.27}\right)$ | Apply the natural log $\ln$ to both sides. |
| $\ln\left(\frac{30000}{369}\right) = \frac{t}{2.27} \ln(2)$ | Use the power rule for logarithms. |
| $\frac{\ln\left(\frac{30000}{369}\right)}{\ln(2)} =\frac{t}{2.27}$ | Divide both sides by $\ln(2)$. |
| $t = 2.27 \frac{\ln\left(\frac{30000}{369}\right)}{\ln(2)}$ | Multiply both sides by $2.27$. |
| $t \approx 14.40$ | Use a calculator to find a decimal approximation. |
So if the number of nuclear warheads since 1950 is given by $f(t)=369(2)^{t/2.27}$, then our work suggests the United States had a stockpile of more than 30,000 warheads some time in the spring of 1964.
QUICK CHECK
If nuclear arms production had continued at that rate, how many warheads would there have been in 2010?Answer
Taking $t=60$, we have [ f(60)=369(2)^{60/2.27} \approx 33,401,528,382 ] which would have been enough for everyone on Earth to have about 5. As of 2017, the official number was 3822 stockpiled warheads according to the US Department of Energy.Population Growth
Suppose your neighbor starts a farm with $4$ cute little rabbits. One hundred days later, she is tending a herd of $28$ rabbits. Assuming exponential growth, how long until she has $500$ rabbits at her farm?
Before we can answer this question, we need to find the continuous rate of growth by solving $28=4e^{k \cdot 100}$ for $k$.
| $28 = 4e^{k \cdot 100}$ | |
|---|---|
| $\frac{28}{4} = e^{100 k}$ | Divide both sides by $4$ to isolate the exponential. |
| $\ln 7 = \ln(e^{100 k})$ | Apply the natural log $\ln$ to both sides. |
| $\ln 7 = 100 k$ | Use the inverse relationship $\ln(e^{x})=x$. |
| $\frac{\ln 7}{100} = k$ | Divide both sides by $100$. |
| $k \approx 0.0195$ | Use a calculator to find a decimal approximation. |
So the number of bunnies can be modeled by $f(t)=4e^{0.0195 \thinspace t}$.
QUICK CHECK
How can we determine when there will be 500 rabbits?Answer
We need to find $t$ so that $f(t)=500$, so we have to solve the equation $500=4e^{0.0195 \thinspace t}$.Since the number of bunnies is modeled by $f(t)=4e^{0.0195 \thinspace t}$, to figure out when the population is at 500 we should solve the equation $500 = 4e^{0.0195 \thinspace t}$ for $t$.
| $500 =4e^{0.0195 \thinspace t}$ | |
|---|---|
| $\frac{500}{4} = e^{0.0195 t}$ | Divide both sides by $4$ to isolate the exponential. |
| $\ln 125 = \ln(e^{0.0195 t})$ | Apply the natural log $\ln$ to both sides. |
| $\ln 125 = 0.0195 t$ | Use the inverse relationship $\ln(e^{x})=x$. |
| $\frac{\ln 125}{0.0195} = t$ | Divide both sides by $0.0195$. |
| $t \approx 247.6$ | Use a calculator to find a decimal approximation. |
We conclude that in roughly 250 days the farmer will have 500 rabbits.
QUICK CHECK
How would the equation have been different if we wanted to know when the farmer would have 2000 rabbits?
Answer
The only change would be that $f(t)=2000$. The solving process would remain the same.Techniques for Solving Logarithmic Equations
While our primary focus has been solving exponential equations that arise from different applications, we should also discuss solving logarithmic equations.
Just as with exponential equations, it's usually best to try and simplify the equation first.
Use Log Properties
If an equation contains multiple logarithms, we should start by using log properties to condense those into a single logarithm, if possible.
For instance, the left side of the equation $\log(x+39)-\log(4x) = 1$ could be condensed using the quotient rule.
[ \begin{align} \log(x+39)-\log(4x) &= 1 \newline \log\left(\frac{x+39}{4x}\right) &= 1 && \small \color{#5fa2ce}{\text{Quotient rule for logs}} \end{align} ]
At this point we can choose an appropriate solving technique from the choices discussed below. But this initial step of trying to condense multiple logarithms is always something we should look for first.
QUICK CHECK
-
Use the product property to write the left side of the equation $\ln 8 + \ln x = 7$ as a single logarithm.
Answer
$\ln(8x)=7$ -
Which log property could you use to simplify the equation $\log(x^{3})=12$?
Answer
The power rule would make the equation $3\log(x)=12$ which becomes the much simpler equation $\log(x)=4$
Solving Method 1: The One-to-One Property of Logarithms
Since logarithms are one-to-one functions, if we know that two logs with the same base are equal then their inputs must also be equal.
[ \log_b(N) = \log_b(M) \text{ if and only if } N=M ]
In other words, as long as both sides are written as single logarithms with the same base, then the logarithms themselves can be ignored.
For example, solving the equation $\log_2(x^{2}+1) = \log_2(26)$ is equivalent to solving $x^{2}+1 = 26$ as we see below.
[ \begin{align} \log_2(x^{2}+1) &= \log_2(26) \newline x^{2}+1 &= 26 && \small \color{#5fa2ce}{\text{One-to-One Property}} \newline x^{2} &= 25 && \small \color{#5fa2ce}{\text{Subtract } 1} \newline x &= \pm 5 && \small \color{#5fa2ce}{\text{Square root both sides}} \end{align} ]
QUICK CHECK
-
Solve the equation $\log_5(x-3) = \log_5(9)$.
Answer
Using the logarithm property of equality, we only need to solve $x-3=9$. The solution is $x=12$. -
Solve the equation $\ln\sqrt{x} = \ln(4)$.
Answer
Using the logarithm property of equality, we only need to solve $\sqrt{x} = 4$. The solution is $x=16$.
Solving Method 2: Rewrite as an Exponential Equation
Another solving technique is to isolate the logarithmic expression and rewrite the equation as an equivalent exponential using the definition of a logarithm.
[ b^{x}=y \Longleftrightarrow \log_{b}(y) = x ]
Consider the equation $4 \log_3(x-2) = 16$. If we divide both sides by $4$ then the logarithm will be isolated and we can solve by rewriting it as an exponential equation.
[ \begin{align} 4 \log_3(x-2) &= 16 \newline \log_3(x-2) &= 4 && \small \color{#5fa2ce}{\text{Divide by } 4} \newline 3^{4} &= x-2 && \small \color{#5fa2ce}{\text{Rewrite as an exponential equation}} \newline 81+2 &= x && \small \color{#5fa2ce}{\text{Add }2} \newline x &= 83 && \small \color{#5fa2ce}{\text{Simplify}} \end{align} ]
This is useful anytime the equation can be written as a single logarithm, even if it doesn't start out that way.
QUICK CHECK
What should be done to isolate the logarithm in the equation $6+\log(2x)=9$?
Answer
Subtracting $6$ from both sides will isolate the logarithm. It can then be solved using the technique above. [ \begin{align} 6+\log(2x) &= 9 \newline \log(2x) &= 3 && \small \color{#5fa2ce}{\text{Subtract } 6} \newline 10^{3} &= 2 x && \small \color{#5fa2ce}{\text{Rewrite as an exponential equation}} \newline \frac{1000}{2} &= x && \small \color{#5fa2ce}{\text{Divide by }2} \newline x &= 500 && \small \color{#5fa2ce}{\text{Simplify}} \end{align} ]Solving Method 3: Exponentiate Both Sides
Our final method is to exponentiate both sides of the equation using the base of the logarithm.
To exponentiate both sides of an equation means to turn each side into an exponent of the base $b$. Once that has been done we can take advantage of the inverse property between logs and exponentials. [ b^{\log_b x} = x ]
We will illustrate the process using the equation $\log_2 x= 6$.
[ \begin{align} \log_2 x &= 6 \newline 2^{\log_{2} x} &= 2^{6} && \small \color{#5fa2ce}{\text{Exponentiate base } 2} \newline x &= 2^{6} && \small \color{#5fa2ce}{\text{Inverse property}} \newline x &= 64 && \small \color{#5fa2ce}{\text{Evaluate}} \end{align} ]
Earlier we would have solved this by rewriting it as the exponential equation $x=2^6$ and simplifying to see that $x=64$, and rewriting is probably the preferred method. We introduce the idea of exponentiation here to reemphasize the inverse relationship between exponentials and logarithms. Not only are they inverse functions, but it can sometimes be useful to think of exponentiation and taking the logarithm as inverse operations. Exponentiating can then be viewed as just another operation we can use when we solve equations by reversing the order of operations.
QUICK CHECK
Exponentiate both sides of the equation $\ln(x) = 4$. Simplify if possible.Answer
The base of the natural logarithm is $e$, so we will place both sides of the equation into the exponent of an $e$. $e^{\ln(x)} = e^{4}$ But $e$ and $\ln$ are inverses, so this simplifies to $x=e^4$ which is the same answer we would get by converting $\ln(x) = 4$ to an exponential equation.Find Inverses
As we learned earlier, we can find an inverse by listing the operations performed by the function and doing the opposite operations in the reverse order. Viewing exponentiation and logarithms as opposite operations allows us to find the inverses of more complicated exponential and logarithmic functions.
For instance, the function $f(x)=5(3)^{x+2}$ does three things to each input value. It adds $2$, then exponentiates with a base of $3$, and lastly multiplies by $5$. It's inverse should divide by $5$, then apply the base $3$ logarithm, and finally subtract $2$. We summarize this in the table below.
| Operations Done by the Function | Operations Done by the Inverse | ||
|---|---|---|---|
| 1. | Add $2$ | 1. | Divide by $5$ |
| 2. | Exponentiate with a base of $3$ | 2. | Apply the base $3$ logarithm |
| 3. | Multiply by $5$ | 3. | Subtract $2$ |
Now we take the operations listed and build the inverse function $f^{-1}$ as follows:
| 1. | Start with a variable: | $x$ |
|---|---|---|
| 2. | Divide by $5$: | $\frac{x}{5}$ |
| 3. | Apply the base $3$ logarithm: | $\log_3\left(\frac{x}{5}\right)$ |
| 4. | Subtract $2$ : | $\log_3\left(\frac{x}{5}\right)-2$ |
| 5. | Write as a function: | $f^{-1}(x)=\log_3\left(\frac{x}{5}\right)-2$ |
QUICK CHECK
Identify the order of operations of the function $f(x)=500(2)^{x/27}$. Then find the inverse function $f^{\thinspace-1}$.Answer
This function (1) divides by 27, then (2) exponentiates with a base of 2, and (3) multiplies by 500. The inverse should (1) divide by 500, (2) apply the base 2 logarithm, and (3) multiply by 27. The equation is $f^{-1}(x)=27*\log_2\left(\frac{x}{500}\right)$.Let's look at another example. This time we will find the inverse of $g(t)=\log_2(3 t-7)$. Start by listing the operations of the function in the proper order and then list which operations its inverse should do.
| Operations Done by the Function | Operations Done by the Inverse | ||
|---|---|---|---|
| 1. | Multiply by $3$ | 1. | Apply the base $2$ exponential |
| 2. | Subtract $7$ | 2. | Add $7$ |
| 3. | Apply the base$2$ logarithm | 3. | Divide by $3$ |
Once we know the inverse operations and their order we can build up the inverse function.
| 1. | Start with a variable: | $t$ |
|---|---|---|
| 2. | Apply the base $2$ exponential: | $2^t$ |
| 3. | Add $7$: | $2^t+7$ |
| 4. | Divide by $3$: | $\frac{2^t+7}{3}$ |
| 5. | Write as a function: | $g^{-1}(t)=\frac{2^t+7}{3}$ |
Looking Ahead
The key idea from this section is that since exponential and logarithmic functions are inverses functions, we can also use them as inverse operations to solve equations and applications.
Additional Practice
Want more practice? Try these optional exercises powered by MyOpenMath. These exercises are purely for practice and are not part of your graded homework - you can attempt them as many times as you'd like!