3.1 Exponential Functions
Introduction
Exponential functions have a type of growth that we have not studied yet, but you have probably seen it before. Perhaps the best place to start is with an example.
The images below illustrate three different real world examples of exponential growth. All three are exactly the same, just in a different context.
 |
 |
 |
|---|---|---|
| Going Viral | Nuclear Reactions | Cell Division |
Exponential Growth
Going Viral

The videos and games on social media sites like YouTube and Facebook can often "go viral" when they experience a rapid increase in popularity.
Imagine, for instance, that you share a video with two friends and each of them shares it with two new friends. If that process continues then the number of new people viewing the video would follow the pattern:
[ 1, 2, 4, 8, 16, 32, 64, \dotsc ]
Notice that these numbers are doubling. One doubles to get two, two doubles to get four, four doubles to get eight, and so on. This type of increase is one example of exponential growth.
If the numbers were to consistently triple, for example $1, 3, 9, 27, \dotsc$, or quadruple like $1,\thinspace 4,\thinspace 16,\thinspace 64,\thinspace \dotsc$, that would also be considered exponential growth.
Nuclear Reactions
 A nuclear reaction begins when a small particle, called a neutron, crashes into an atom and splits it in half. When that atom splits it releases more neutrons. Those neutrons crash into other atoms and cause them to split as well.
A nuclear reaction begins when a small particle, called a neutron, crashes into an atom and splits it in half. When that atom splits it releases more neutrons. Those neutrons crash into other atoms and cause them to split as well.
If each atom that splits causes two more atoms to split, then the number of reactions would follow the pattern:
[ 1, 2, 4, 8, 16, 32, 64, \dotsc ]
Notice that these numbers are doubling. One doubles to get two, two doubles to get four, four doubles to get eight, and so on. This type of increase is one example of exponential growth.
If the numbers were to consistently triple, for example $1, 3, 9, 27, \dotsc$ or quadruple like $1,\thinspace 4,\thinspace 16,\thinspace 64,\thinspace \dotsc$, that would also be considered exponential growth.
Cell Division
 All living cells reproduce by cell division. Once a cell matures, it then splits into two new cells. These new cells can also split once they mature.
All living cells reproduce by cell division. Once a cell matures, it then splits into two new cells. These new cells can also split once they mature.
The number of cells would follow the pattern:
[ 1, 2, 4, 8, 16, 32, 64, \dotsc ]
Notice that these numbers are doubling. One doubles to get two, two doubles to get four, four doubles to get eight, and so on. This type of increase is one example of exponential growth.
If the numbers were to consistently triple for example $1, 3, 9, 27, \dotsc$, or quadruple like $1,\thinspace 4,\thinspace 16,\thinspace 64,\thinspace \dotsc$, that would also be considered exponential growth.
Exponential Decay

In the 2010 FIFA World Cup, teams from 16 countries competed for the world championship of men's soccer.
In each round, the losing teams were eliminated from the tournament while the winners advanced to the next round. This process continued until there was only one undefeated champion: the Spanish national team. The number of teams in each round followed the pattern:
[ 16, 8, 4, 2, 1 ]
Notice that these numbers are always halving. One-half of sixteen is eight, one-half of eight is four, and so on. This type of decrease is an example of exponential decay.
If each number was always one-third or one-fifth of the previous number (for example $27, 9, 3, 1\thinspace$ or $\thinspace250, 50, 10, 2$) then that would also be considered exponential decay.
Linear vs. Exponential
These examples show us that exponential growth is special because each new value is a multiple of the previous one. Contrast this with linear growth where each new value is the previous value plus a constant.
With linear growth, the number you add to move from one value to the next is called the slope and is usually represented by the letter $m$. In exponential growth, the number we multiply by to move from one value to the next is called the growth factor. We will use the letter $b$ to represent the growth factor.
QUICK CHECK
-
Are the values $5,\thinspace 10,\thinspace 15,\thinspace 20, ...$ growing linearly or exponentially?
Answer
Each new value is the previous one plus $5$, so this is linear growth. -
Are the values $5,\thinspace 25,\thinspace 125,\thinspace 625, ...$ growing linearly or exponentially?
Answer
Each new value is the previous one times $5$, so this is exponential growth. -
Suppose a list of numbers grows exponentially with a growth factor of $b=3$. How would you find the next value in the list?
Answer
Each new number would be $3$ times the prior one.
Recall that the only difference between linear growth and linear decay is the sign of the slope. If $m$ is positive, the line increases, or grows. But if $m$ is negative, the line decreases, or decays.
In a similar way, the only difference between exponential growth and exponential decay is the value of the growth factor $b$. Growth occurs when $b$ is large, whereas the function decays if $b$ is small. Specifically, any growth factor $0<b<1$ will result in exponential decay.
If we know for certain that $0<b<1$, then we call $b$ a decay factor. If no value of $b$ is specified, then we will use the term growth factor in a generic sense that could include the possibility of growth or decay.
QUICK CHECK
Decide if the following tables display exponential growth or decay. Then state the value of the growth factor.
| $90$ | $30$ | $10$ | $\frac{10}{3}$ | $\frac{10}{9}$ |
|---|
Answer
Each new value is the previous one multiplied by $\frac{1}{3}$, so this is exponential decay with a growth factor of $b=\frac{1}{3}$.| $\frac{7}{16}$ | $\frac{7}{4}$ | $7$ | $28$ | $112$ |
|---|
Answer
Each new value is the previous value times $4$, so this is exponential growth with $b=4$.Identify Characteristics of Exponential Functions
Now that we can identify exponential growth, it's time to derive the basic equation for an exponential function.
Our first growth examples in this section followed the pattern $1, 2, 4, 8, 16, 32, 64,\dotsc$ where the growth factor is $b=2$ and each new value is twice the previous value. If we recall that $1=2^0$, then a clear pattern emerges.
Using function notation we might write this as $f(x) = 2^{x}$, which is nothing more than the growth factor $b=2$ raised to the power of $x$. This gives us a clue for how the basic equation of an exponential function should look.
All exponential functions, whether they represent growth or decay, have the same basic form. The basic form for an exponential function is
[ f(x) = b^{x} ]
The base of the function is the growth factor $b$, which can be any positive number.
We should be careful not to confuse an exponential function $f(x)=b^{x}$ with a power function $f(x)=x^{p}$. Even though their equations look similar, they are completely different types of functions. The key difference is that an exponential function has a variable $x$ in the exponent, whereas the exponent of a power function is a fixed constant.
QUICK CHECK
Are any of the following exponential functions? If so, identify the base $b$ and decide if the function grows or decays as $x$ increases.
-
$f(x)=3^{x}$
Answer
Yes, this is an exponential function with $b=3$. Since $b>1$ the function will grow as $x$ increases. -
$h(t)=t^{2}$
Answer
No, the variable needs to be in the exponent. This is actually a power function. -
$g(x)=(1/5)^{x}$
Answer
Yes, this is an exponential function with $b=1/5$. Since $0<b<1$ the value of the function will decay as $x$ increases. -
$Q(x)=x^{0.2}$
Answer
No, this is not an exponential function. It is actually a power function. -
$P(t)=(-2)^t$
Answer
No, this is not an exponential function. The base of an exponential function must be positive.
The shape of the graph of an exponential function is controlled entirely by the value of the base $b$. In the following figure you can change the value of the base $b$ by moving the blue slider. As you do so, pay attention to the shape of the graph.
You should specifically check for each of the following behaviors, which were introduced in Chapter 1.
Behaviors
- Domain includes all $x$ values; the Range is $y>0$.
- All exponential functions have the same y-intercept of $y=1$. There are no x-intercepts since exponential functions never cross the x-axis.
- If $b > 1$ the function is always increasing and represents exponential growth. Larger values of $b$ produce faster growth. If $0 < b < 1$ the function is always decreasing and indicates exponential decay. The decay is greatest when $b$ is close to $0$. When $b=1$ the function is constant and is usually not considered exponential.
- Exponential functions are either always increasing or always decreasing. They do not have any maximums or minimums.
- Exponential functions are always concave up.
- The x-axis is a horizontal asymptote, but there are no vertical asymptotes.
- Exponential functions do not have odd or even symmetry.
- All exponentials are one-to-one. This means that every exponential function must have an inverse, which will be called a logarithm.
Evaluate Exponential Functions
When we want to evaluate an exponential function we can often take advantage of the rules of exponents. For instance, if $f(x)=2^{x}$ then
[ f(-3/2) = 2^{-3/2} = \frac{1}{\sqrt{2^{3}}} = \frac{1}{2\sqrt{2}} ]
This is an exact expression for $f(-3/2)$. Sometimes it may make sense to use a calculator to find an approximate decimal value instead. In this case, $f(-3/2) \approx 0.3536$.
QUICK CHECK
Give exact values for the following. Use the rules of exponents as needed.
-
$3^{-2}$
Answer
$\frac{1}{3^2}=1/9$ -
$5^{1/2}$
Answer
$\sqrt{5}$ -
$2^{0}$
Answer
$1$
Use a calculator to approximate the following:
-
$\left(\frac{1}{2}\right)^{1.6}$
Answer
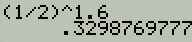
-
$1.5^{\pi}$
Answer

-
$\left(1+\frac{0.8}{12}\right)^{(12 \cdot 7)}$
Answer
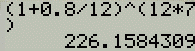
How Exponential Functions Change
We said earlier that exponential functions $f(x)=b^{x}$ are special because each time $x$ increases by $1$ the value of the function is multiplied by a factor of $b$. In other words, if $f$ is an exponential function, then
[ f(x+1)=b \cdot f(x) ]
You'll recall that this pattern was the key to identifying exponential growth and decay.
This simple property, $f(x+1)=b \cdot f(x)$, is unique to exponential functions and causes them to change in a way that is different than any other type of function.
Consider, for example, the percent change of an exponential function $f$ over the interval $[x,\thinspace x+1]$.
| Percent change | [ \frac{f(x+1)-f(x)}{f(x)} ] | Percent change formula. |
|---|---|---|
| [\frac{b \cdot f(x)-f(x)}{f(x)}] | Apply the property $f(x+1)=b \cdot f(x)$. | |
| [b-1] | Cancel the $f(x)$. |
Since $b$ is constant, $b-1$ is also constant. This means that the percent change from one value to the next is always constant. Having a constant percent change is one of the features that distinguishes exponential functions from all other functions.
QUICK CHECK
- The percent changes for two functions, $f$ and $g$, are shown below.

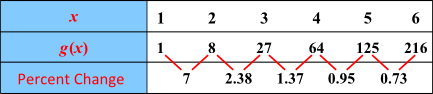
Which one is an exponential function?Answer
The first function $f$ is exponential because its percent change is constant. The second function $g$ is likely a power function, since its percent change is decreasing.
For any exponential function $f(x)=b^{x}$ with a growth factor of $b$, the expression $b-1$ is called the growth rate of the function and is designated by the letter $r$. For instance, if $f(x)=1.08^{x}$, where $b=1.08$, then the growth rate is $r=0.08$.
To see why the growth rate is important, let's take a look at the total change of a basic exponential function over the interval $[x, \thinspace x+1]$.
| $\Delta y$ | $= f(x+1)-f(x)$ | Total change formula. |
|---|---|---|
| $=b \cdot f(x)-f(x)$ | Apply the property $f(x+1)=b \cdot f(x)$. | |
| $=f(x) (b-1)$ | Factor out $f(x)$. | |
| $=r \cdot f(x)$ | Substitute $r=b-1$. |
This result indicates that difference between $f(x)$ and $f(x+1)$ is $r \cdot f(x)$. In other words, to move from one value to the next you add $r$ times the current function value.
For instance, if $b=1.08$, then $f(x+1)=f(x) + .08f(x)$, meaning that every time $x$ increases by $1$, the function increases by $8\text{%}$.
QUICK CHECK
- Suppose $f(x)=1.26^{x}$. Identify both the growth factor $b$ and the growth rate $r$.
Answer
The growth factor is the base $b=1.26$. The growth rate is $r=0.26$, meaning the every time $x$ increases by $1$ the function increases by $26\text{%}$.
Difference Quotients of Exponentials
The difference quotient of an exponential function $f(x)=b^{x}$ can be simplified as follows:
| $D(x)$ | $= \frac{f(x+h)-f(x)}{h}$ | Difference quotient formula. |
|---|---|---|
| $= \frac{b^{x+h}-b^{x}}{h}$ | Insert $f(x+h)=b^{x+h}$ and $f(x)=b^x$. | |
| $= \frac{b^{x} b^{h}-b^{x}}{h}$ | Rewrite $b^{x+h}$ as $ b^{x} b^{h}$. | |
| $= b^{x} \left( \frac{b^{h}-1}{h} \right)$ | Factor out $b^{x}$. |
Since $b$ and $h$ are constants, the expression $\frac{b^{h}-1}{h}$ is also a constant. This means that the difference quotient of any exponential function is always proportional to the function itself.
This is certainly different from what we observed with power functions. The difference quotient of a power function is related to a power function with a lower degree, not to the function itself. For instance $x^{3}$ grows at a rate involving $x^{2}$. Only exponential functions grow at rates proportional to themselves.
Let's consider a specific example. If $f(x)=10^{x}$ then the difference quotient is
| $D(x)$ | $= b^{x} \left( \frac{b^{h}-1}{h} \right)$ | Use the result from above. |
|---|---|---|
| $= 10^{x} \left( \frac{10^{h}-1}{h} \right)$ | Insert the growth factor $b=10$. |
This shows that no mater which $h>0$ we choose, $D(x)$ will always be a multiple of the original function $f(x)=10^{x}$. For instance, choosing $h=1$ gives
[ D(x) = \left( \frac{10^{1}-1}{1} \right) 10^{x} = 9 \cdot 10^{x} ]
QUICK CHECK
-
What is the difference quotient of $f(x)=3^{x}$.
Answer
Inserting $b=3$ into the formula above we see that $D(x)=\left(\frac{3^{h}-1}{h}\right) 3^{x}$ -
Evaluate with the difference quotient of $f(x)=3^{x}$ with $h=2$.
Answer
If $h=2$ then $D(x)=\left(\frac{3^{2-1}}{2}\right) 3^{x}=4 \cdot 3^{x}$ In other words, the difference quotient is the original function times $4$.
The Number e
Since every exponential function is proportional to its difference quotient, it's possible that there are special cases where the function and the difference quotient are identical. To pinpoint when this might happen, let's reexamine the equation for the difference quotient of $f(x)=b^{x}$.
[ D(x) = \frac{b^{h}-1}{h} b^{x} ]
Notice that if $\frac{b^{h}-1}{h}=1$, then $D(x)=b^{x}=f(x)$. In other words, if we can find values of $b$ and $h$ that make $\frac{b^{h}-1}{h}=1$, then the difference quotient will equal the function.
Although there are many combinations of $b$ and $h$ that make $\frac{b^{h}-1}{h}=1$, the most important one arises when $h$ is chosen to be a very small, positive number. In the interactive figure below, we have fixed $h = 0.001$. Use the slider to adjust the value of $b$ until you find one where $\color{red}{D(x)}=f(x)$.
Which value of $b$ works? From the figure it appears that choosing $b$ somewhere around $2.718$ does the trick.
The true value is an irrational number known as $e$. Since $e$ is an irrational number, $2.718$ is just an approximation of it, much like $3.14$ is an approximation of $\pi$. Before we can find more precise approximations of $e$, we need to define exactly what $e$ is.
The number $e$ was discovered by a Swiss mathematician, Jacob Bernoulli, as he studied interest on loans, an application we will look at in the next section. The name $e$ was given by another Swiss mathematician, Leonard Euler.
While there are many ways to define $e$, we choose to say that $e$ is the number which causes $\frac{b^h-1}{h}=1$ as $h \rightarrow 0$. Solving this equation for $b$ will give us a variation of the formula Bernoulli used to discover $e$.
| $\frac{b^h-1}{h} = 1$ | Original equation. |
|---|---|
| $b^h-1 = h$ | Multiply both sides by $h$. |
| $b^h = 1+h$ | Add $1$ to both sides. |
| $b = (1+h)^{1/h}$ | Take the $1/h$ power. |
As $h>0$ approaches zero, this expression approaches the number $e$. That is to say,
[ (1+h)^{1/h} \rightarrow e \thinspace \text{ as } \thinspace h \rightarrow 0 ]
which is equivalent to one of the definitions Euler used.
The fact that $(1+h)^{1/h} \rightarrow e$ as $h \rightarrow 0$ allows us to find more precise approximations of $e$ by simply making $h$ closer to $0$.
| $h$ | $(1+h)^{1/h}$ |
|---|---|
| $0.01$ | $2.70481$ |
| $0.0001$ | $2.71815$ |
| $0.000001$ | $2.71828$ |
| $0.00000001$ | $2.71828$ |
Euler once approximated $e$ out to 18 decimal places as $2.718281828459045235$, all by hand. You do not need to memorize several digits of $e$, but remembering that $e \approx 2.718$ will give you a good approximation for making rough calculations.
Today $e$ is considered one of the most important numbers in mathematics and science. It is used so frequently, that the exponential function with a base of $e$ is often called the exponential function, as though no other bases mattered. You will find that your calculator as a button dedicated to evaluating $e^{x}$ for any real number $x$.
QUICK CHECK
Find the $e^{x}$ button on your calculator and use it to evaluate the following:
-
$e^{2}$
Answer
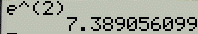
-
$e^{-3.4}$
Answer
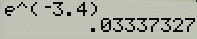
-
$60 e^{-.035(15)}$
Answer
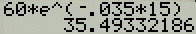
-
Does $f(x)=e^{x}$ represent exponential growth or decay? What about $f(x)=e^{-x}$?
Answer
Since $e>1$, it follows that $f(x)=e^{x}$ is an exponential growth function. However, $0<1/e<1$, so $f(x)=e^{-x}=(1/e)^{x}$ is an exponential decay function.
Looking Ahead
In the next section we will see several applications of exponential functions, and many of those will involve using the number $e$ as the base of an exponential function.
Additional Practice
Want more practice? Try these optional exercises powered by MyOpenMath. These exercises are purely for practice and are not part of your graded homework - you can attempt them as many times as you'd like!



