1.4 Transformations of Functions
Introduction
When making ice cream, chefs often start with a basic recipe and then add in different amounts of special ingredients, like macadamia nuts or dark chocolate or berries. Experienced chefs know the effect that each addition will have before they even taste the finished product.
In a very similar way, we can take basic functions and transform them into new functions by mixing in constants. As you gain experience you will be able to predict the behavior of a transformed function without graphing it. You will also learn to construct the equation for a function given its graph.
Given a generic function $f$ and any constant number $\color{blue}{c}$, there are four ways to combine them to form a new function. We could
| 1. | Add $\color{blue}{c}$ to the function value $f(x)$. | $f(x)+\color{blue}{c}$ |
|---|---|---|
| 2. | Add $\color{blue}{c}$ to the input value $x$. | $f(x+\color{blue}{c})$ |
| 3. | Multiply $f(x)$ by $\color{blue}{c}$. | $\color{blue}{c} \thinspace f(x)$ |
| 4. | Multiply $x$ by $\color{blue}{c}$. | $f(\color{blue}{c} \thinspace x)$ |
We will use interactive figures to explore each of these combinations. Pay special attention to how both the graph and the equation change as you apply the transformation. It may even help to keep track of one or two points and compare their locations before and after the transformation.
Vertical Shifts
The first transformation we want to look at is adding a constant $\color{blue}{c}$ to the output of the function, $f(x)$.
In this figure you can change the value of $\color{blue}{c}$. The graph of the original function $\color{black}{f(x)}$ is shown in $\color{black}{black}$. The transformed function $\color{red}{f(x)} \color{blue}{+ c}$ will be shown in $\color{red}{red}$.
How would you describe the relationship between the two graphs?

To use the interactive figure visit https://www.geogebra.org/m/Y5TzgBaP
The result of adding a constant to a function is that the graph moves up or down $\color{blue}{c}$ spaces.
More formally, if $\color{red}{f}$ is any function and $\color{blue}{c}$ is any constant, then the graph $\color{red}{f(x)} \color{blue}{+ c}$ is a vertical shift of the function $f$. The graph of $\color{red}{f(x)} \color{blue}{+ c}$ can be found by adding $\color{blue}{c}$ to every y-value of the original graph. We can summarize this by saying
- If $\color{blue}{c>0}$, then $\color{red}{f(x)} \color{blue}{+ c}$ is found by shifting the graph of $f$ up $\color{blue}{c}$ spaces.
- If $\color{blue}{c<0}$, then $\color{red}{f(x)} \color{blue}{+ c}$ is found by shifting the graph of $f$ down $\color{blue}{c}$ spaces.
QUICK CHECK
-
How is the graph of $y=\sqrt{x}+10$ different from the graph of $f(x)=\sqrt{x}$ ?
Answer
The graph of $y=\sqrt{x}+10$ has the same shape as the graph of $f(x)=\sqrt{x}$, except that it has been shifted up $10$ spaces. -
What function would have the same shape as $f(x)=x^{2}$ but shifted $6$ spaces up?
Answer
$f(x)+6 = x^{2}+6$
Horizontal Shifts
Another way to transform a function is to add a constant $\color{blue}{c}$ to the input $x$. Use the figure to observe what happens to $\color{red}{f(x }\color{blue}{+ c} \color{red}{)}$ as the value of $\color{blue}{c}$ changes.
Pay special attention to the sign of $\color{blue}{c}$. Which direction is the transformation when $\color{blue}{c}$ is positive?

To use the interactive figure visit https://www.geogebra.org/m/YJUZlyHJ
- If $\color{blue}{c>0}$, then $\color{red}{f(x} \color{blue}{+ c}\color{red}{)}$ is found by shifting $f$ to the left $\color{blue}{c}$ spaces.
- If $\color{blue}{c<0}$, then $\color{red}{f(x } \color{blue}{+ c}\color{red}{)}$ is found by shifting $f$ to the right $\color{blue}{c}$ spaces.
Horizontal shifts are somewhat counter intuitive, and you will want to refer back to this chart often as you work through the exercises.
Vertical and horizontal shifts do not change the shape of the graph, only its location. Our next few transformations, however, will alter the shape of the graph.
QUICK CHECK
Suppose the function $P(h)$ gives your weekly pay based on the number of hours worked.
-
Describe what the graph of $P(h+10)$ would look like, and what it would mean.
Answer
$P(h+10)$ is a shift left 10 spaces. It corresponds to getting paid for 10 extra hours of work.
If you worked 15 hours, for example, then you would be paid for 25 hours of work. -
Describe what the graph of $P(h-10)$ would look like, and what it would mean.
Answer
$P(h-10)$ is a shift right 10 spaces. It would represent being paid for 10 fewer hours.
For instance, if you worked for 40 hours, you would only be paid for 30. -
What function would have the same shape as $f(x)=x^{2}$ but shifted $4$ spaces horizontally to the left?
Answer
$f(x+4) = (x+4)^2$
Vertical Stretches
The two previous transformations involved addition and resulted in a shift. Using the figure below, you can discover the effect of multiplying a function by a positive constant $\color{blue}{c}$. As you change the value of $\color{blue}{c}$ , the graph of $\color{blue}{c}\color{red}{ f(x)}$ will change as well. How would you describe this change?

To use the interactive figure visit https://www.geogebra.org/m/HJhxc4Lx
Hopefully you noticed that multiplying a function by a constant $\color{blue}{c}$ stretches the graph up and down.
In other words, if $\color{red}{f}$ is any function and $\color{blue}{c}$ is any constant, then the graph of $\color{blue}{c}\color{red}{ f(x)}$ is a vertical stretch of the original function $\color{red}{f}$. The graph of $\color{blue}{c}\color{red}{ f(x)}$ can be found by multiplying each y-value of the original graph by $\color{blue}{c}$.
If $\color{blue}{0<c<1}$, then the graph $\color{blue}{c}\color{red}{f(x)}$ is sometimes called a vertical compression of the graph of $\color{red}{f}$. We will use the word stretch for both situations, with the understanding that the graph is always scaled by a factor of $\color{blue}{c}$.
QUICK CHECK
-
Suppose $(2, 5)$ is a point on the graph of the function $\color{red}{f}$. What does the transformation $\color{blue}{4}\color{red}{f(x)}$ do to that point?
Answer
The transformation multiplies the y-value by a factor of $\color{blue}{4}$ transforming the point $(2, 5)$ into $(2, 20)$. -
Suppose $(3, 8)$ is a point on the graph of the function $\color{red}{g}$. What does the transformation $\color{blue}{0.5}\color{red}{g(x)}$ do to that point?
Answer
The transformation multiplies the y-value by a factor of $\color{blue}{0.5}$, transforming the point $(3, 8)$ into $(3, 4)$. -
What function would look like $f(x)=x^{2}$ but stretched vertically by a factor of $5$?
Answer
$5f(x) = 5 x^{2}$
Horizontal Stretches
A function can be stretched horizontally by multiplying the input $x$ by some constant $\color{blue}{c}$. Use the following interactive figure to observe how the shape of the graph changes for different values of $\color{blue}{c}$.
How much wider is the function when $\color{blue}{c = 2}$ as compared to when $\color{blue}{c = 0.5}$?

To use the interactive figure visit https://www.geogebra.org/m/ZPBnPTlS
This horizontal stretch is one of the most counter-intuitive transformations you will encounter. You should have seen that the graph got wider when $\color{blue}{c}$ was small, and narrower when $\color{blue}{c}$ was large.
When we encounter a transformation of the form $\color{red}{f (} \color{blue}{c}\thinspace \color{red}{x)}$, its graph can be found by dividing each x-value of the original graph by $\color{blue}{c}$.
- If $\color{blue}{c>1}$, then the resulting graph is compressed horizontally.
- If $\color{blue}{0<c<1}$, then the resulting graph is stretched horizontally.
In either case, the x-values are always scaled by a factor of $\color{blue}{1/c}$.
QUICK CHECK
-
Suppose that the graph of the function $f (x)$ below describes the path of an average drive by PGA professional Stewart Cink using his current golf club.
 Imagine that a new club has been developed that will transform $f(x)$ into $f(2 x)$. What would this new club do to the distance of his drive?
Imagine that a new club has been developed that will transform $f(x)$ into $f(2 x)$. What would this new club do to the distance of his drive? Answer
$f(2 x)$ is a horizontal stretch with $c=2$. Since $c=2>1$, this will actually compress the graph horizontally, cutting the distance in half.
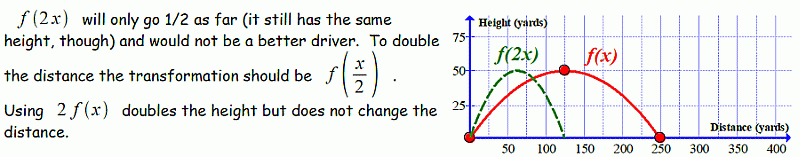
If the goal was to double the distance, the transformation would need to be $f\left(\frac{1}{2}x\right)$. -
What function would look like $f(x)=x^{2}$ but horizontally stretched by a factor of $3$?
Answer
$f\left(\frac{x}{3}\right) = \left(\frac{x}{3}\right)^2$
Vertical and Horizontal Reflections
The last category of transformations we will study are the reflections. The graph of $-f(x)$ is a vertical reflection of the function $f$ across the x-axis. In a vertical reflection all of the y-coordinates change signs from positive to negative or vice versa.

To use the interactive figure visit https://www.geogebra.org/m/ae4EaVFq
The graph of $f(-x)$ is a horizontal reflection of $f$ across the y-axis With horizontal reflections the x-coordinates change signs.

To use the interactive figure visit https://www.geogebra.org/m/xQwb021E
Notice that these transformations follow the pattern of inside/outside changes we've seen before. Putting the negative sign outside the function causes a vertical reflection, while a negative inside the function produces a horizontal reflection.
QUICK CHECK
-
Find the equation of a function whose graph looks similar to $f(x)=\sqrt{x}+3$, except reflected across the x-axis.
Answer
$y=-\sqrt{x}-3$. -
Find the equation of a function whose graph looks similar to $f(x)=\frac{1}{x-2}$, except reflected across the y-axis.
Answer
$y=\frac{1}{-x-2}$.
Identifying Transformations
The six transformations we have discussed so far are summarized below.
| Transformation | Description | Coordinate Change |
|---|---|---|
| $f(x)\color{blue}{+c}$ | Vertical Shift | $(x, y) \rightarrow (x \thinspace , \thinspace y+\color{blue}{c})$ |
| $f(x\color{blue}{+c})$ | Horizontal Shift | $(x, y) \rightarrow (x-\color{blue}{c} \thinspace , \thinspace y)$ |
| $\color{blue}{c} \thinspace f(x)$ | Vertical Stretch | $(x, y) \rightarrow (x \thinspace , \thinspace \color{blue}{c} \thinspace y)$ |
| $f(\color{blue}{c} \thinspace x)$ | Horizontal Stretch | $(x, y) \rightarrow \left(\frac{x}{\color{blue}{c}} \thinspace , \thinspace y\right)$ |
| $\color{blue}{-}f(x)$ | Vertical Reflection | $(x, y) \rightarrow (x \thinspace , \thinspace \color{blue}{-}y)$ |
| $f(\color{blue}{-}x)$ | Horizontal Reflection | $(x, y) \rightarrow (\color{blue}{-}x \thinspace , \thinspace y)$ |
Notice that the location of the constant indicates whether the transformation is vertical or horizontal. Changes outside the function alter the y-coordinate and result in vertical transformations, while changes inside the function impact the x-coordinate and cause horizontal transformations.
Furthermore, you can determine if the transformation is a shift or a stretch by looking at the operation. Shifts are addition, stretches are multiplication. Horizontal transformations always behave in a counter intuitive way, so you will want to be extra careful with them.
QUICK CHECK
What is the difference between $2f(x)$, $ f(2x)$ and $ f(x)+2$ ?Answer
$2f(x)$ means to multiply each $f(x)$ value by $2$, resulting in a vertical stretch by a factor of $2$. $f(2x)$ means to use $2 x$ as the input to the function $f$. The result is a horizontal compression by a factor of $1/2$. $f(x)+2$ means we add $2$ to each $f(x)$ value, which shifts the graph vertically $2$ spaces.Symmetry
Combining a horizontal reflection with a vertical reflection creates a reflection around the origin.
The interactive figure below allows you to compare the horizontal reflection of a point across the y-axis with a reflection around the origin. Choose the reflection(s) you want to see and move the blue pont. As you do so, the location of the points will be traced, creating an image that has symmetry. Experiment with this for a while before continuing.

To use the interactive figure visit https://www.geogebra.org/m/iHmotfOF
Even and Odd Symmetry
When reflecting a graph, two interesting things happen sometimes. The first is that a horizontal reflection across the y-axis might produce the same exact graph as the original function. Symbolically, $f(-x)=f(x)$. When this happens we say that the function has even symmetry, or is symmetric across the y-axis. The figure below illustrates the concept.

To use the interactive figure visit https://www.geogebra.org/m/mSp9DhKO
The other interesting thing that can happen with reflections is that a horizontal reflection and a vertical reflection might have the same result, that is $f(-x)=-f(x)$. When this happens the function has odd symmetry and is symmetric around the origin. Visually, a 180-degree rotation around the origin produces the same exact image. This is illustrated in the following interactive figure.

To use the interactive figure visit https://www.geogebra.org/m/DpMbG1ID
QUICK CHECK
Describe the symmetry of the following graphs.
-

Answer
Odd symmetry -

Answer
Even symmetry -

Answer
Odd symmetry -

Answer
This graph does not have even or odd symmetry. Had it been centered along the y-axis, then it would have had even symmetry. -

Answer
This graph does not have even or odd symmetry. If it were centered at the origin, then it would have had odd symmetry.
Verifying Symmetry Algebraically
While visual identification of symmetry is quick and easy, our eyes can sometimes be deceived. If a function is defined by an equation, then it is best to verify symmetry algebraically. If a function is even, then we should be able to demonstrate that the equations for $f(-x)$ and $f(x)$ are the same. If has odd symmetry, then the equations for $f(-x)$ and $-f(x)$ should be identical.

Consider the graph of $f(x)=x^3+0.01$, which appears to have odd symmetry. Checking the equations we find that
[ f(-x) = (-x)^3+0.01 = -x^3+0.01 ]
while
[ -f(x) = -(x^3+0.01) = -x^3-0.01 ]
Since the two equations are not the same, $f(x)=x^3+0.01$ does not have odd symmetry.
A second look at the equation explains why this is the case. Notice that $f(x)=x^3+0.01$ is nothing more than the cube function shifted $0.01$ units up. It's graph

does not go through the origin, rather it has a y-intercept at $(0, 0.01)$. It is this small shift that causes the function to loose its odd symmetry.
Let's look at one more example. The graph of $f(x)=x^{2}-1$ looks like it has even symmetry.

To check this algebraically, we need to compare the equation for $f(-x)$ with the equation for $f(x)$. If the two match, then it really does have even symmetry. Otherwise, it does not.
Replacing $x$ with $-x$ we find that
[ f(-x) = (-x)^2-1 = x^{2}-1 ]
which is exactly the same equation as $f(x)$. Since $f(-x)=f(x)$, we can confidently conclude that $f(x)=x^{2}-1$ has even symmetry.
Looking Ahead
In future chapters, we will find transformations included in the standard forms of several function models. Being able to predict the effects of a shift or stretch will often simplify calculations and may give insight into easier techniques for solving equations.
Transformations will be helpful when we model data in Chapter 6. If a data set looks like a line, for example, then we can apply shifts and stretches to the identity function $f(x)=x$ until we find a combination that fits the shape of the data.



